3 ブロック化フロイド・ワーシャル法 反復型BFW法8) は隣接行列M をt×t のタイルに分割し,各タイルの更新を反復する. 行列要素Mu,v はグラフG 上の頂点u およびv 間の辺の重みを表す.u からv への最短路(の長さ)を求める.グリーディ法 (貪欲算法)による. • ワーシャル・フロイドのアルゴリズム すべての2 頂点間の最短路(の長さ)を求め る.動的計画法による. ------------------ (a) ダイクストラのアルゴリズムダイクストラ法 開始時間ms 終了時間ms ワーシャルフロイド法(その3) 開始時間84ms 終了時間91ms 速度比率 倍
貝合わせ 箔 名古屋帯 マトラッセ 正絹 中古 袋帯 秀品 草花 美品 和服 店ランクa リサイクル バイセルオンライン ベージュ 帯 送料無料 夏休み 夏祭り 海 山 花火大会 ギフト 贈り物 プレゼント 誕生日 記念日 結婚式 ブライダル ファッション 旅行
ワーシャル-フロイド法
ワーシャル-フロイド法- · ④頂点i から 頂点j に行く移動距離と、頂点i から 頂点k を経由して 頂点j に行く移動距離を比べ、小さい方を 頂点i~頂点j の移動距離として上書きする(29) ←この操作がワーシャルフロイド法におけるもっとも重要な部分!0406 · ワーシャルフロイド法を使って、 他の頂点を経由した方が距離が短くなる場合は1、 別の経由地を使って最短距離と同じになる場合はその2点間のエッジを切ればよいです。




作題 問題文 テスタ I Sports Days 2 0 テスタ Ppt Download
0211 · ワーシャルフロイド法? アルゴリズムの一種らしい。 ワーシャル–フロイド法(英 Warshall–Floyd Algorithm)は、重み付き有向グラフの全ペアの最短経路問題を多項式時間で解くアルゴリズムである。 名称は考案者であるスティーブン・ワーシャル(英語版)とロバート・フロイドに · ワーシャルフロイドとは? 全ノードの最短経路をo(n^3)で実現出来る素晴らしいアルゴリズム。 このアルゴリズムの特徴はなんと言っても数行で全てのノード間の最短経路が求められるとワーシャルフロイド法 ワーシャルフロイド法は、グラフの全ての頂点の間の最短路を見つけるアルゴリズム。 「3つの頂点a, b, cを選んで、a→b→cという道がa→cという道より短ければa→cの距離を更新する」 という操作を全ての頂点の組み合わせで繰り返して最短距離を確定させていく。 (a→b→cやa→cの道が存在しないときは、距離が無限大の道があると考え、a
1714 · D問題 アルゴリズム • ワーシャルフロイド法の実装 – 非常に簡単、以下のようなアルゴリズムで実装可能! – 各点同士の距離を表す配列distには、あらかじめ、以下のよう に数字設定をする • distii = 0; · AtCoder Beginner Contest 051のD問題を解こうとしたらワーシャルフロイド法に出会ったので実装してみました。 abc051contestatcoderjpワーシャル–フロイド法(英 Warshall–Floyd Algorithm)は、 重み付き有向グラフの全ペアの最短経路問題を多項式時間で解くアルゴリズムである。 名称は考案者であるスティーブン・ワーシャルとロバート・フロイドにちなむ(二人はそれぞれ独立に考案)。
1710 · ワーシャルフロイド法 (ダイクストラは個別ルートでは早いが、先に全ルート計算しておくなら、 こっちの方法の法が速いこともある) と、 STLのリストの使い方 (ファンクションへのリストの渡し方とか、リストの複製の作り方とか) などの、便利な技が仕込まれているので貼っておく #include #include #include #include using namespace std · 全点対間最短経路問題 (APSP All Pairs Shortest Path)を解くアルゴリズムのひとつにワーシャルフロイド法がある。 特徴: Gに負の閉路がない限り、Gに負の重みをもつ辺が存在しても適用可。 Gに負の閉路があるかどうかの判定に使える。すなわち、ある頂点vから頂点v(それ自身)への最短距離が負にフロイド・ワーシャル法 百科事典 ナビゲーションに移動 検索に移動 最短経路問題 > ワーシャル–フロイド法 ワーシャル–フロイド法 (英 Warshall–Floyd Algorithm)は、重み付き有向グラフの全




最短経路問題の意味 用法を知る Astamuse
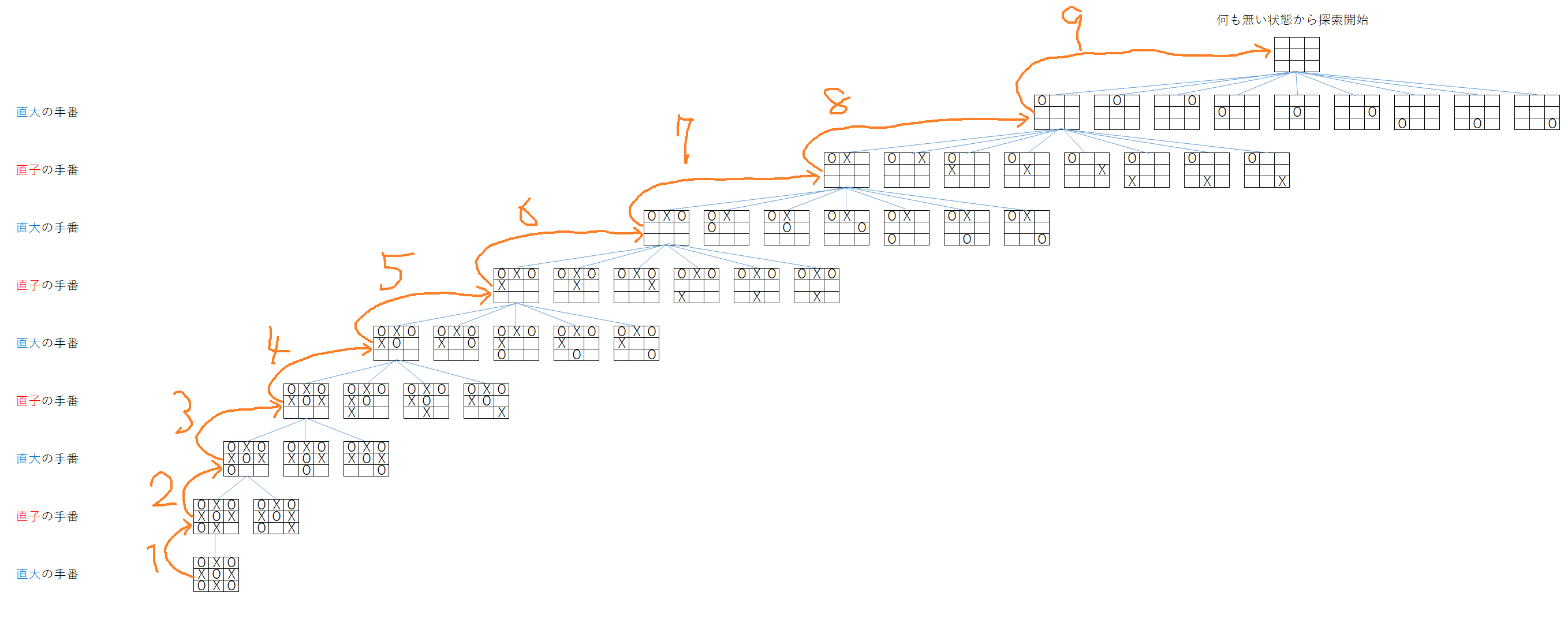



Abc C第5弾 Qiita
· D Wall 配点 400 400 点 問題文 魔法少女のjoisinoお姉ちゃんは、この世にあるすべての数字を 1 1 に変えてやろうと思い立ちました。 1 1 つの数字を i i から j ( 0 ≦ i, j ≦ 9) j ( 0 ≦ i, j ≦ 9) に書き変えるには魔力 c i, j c i, j が必要です。 今、目の前にあるワーシャルフロイド法というアルゴリズムを用いると、o (n3) で全点間の最短距離を求めること が出来ます。 まず、各町を頂点とし、各道を辺とした重み付き無向グラフを作ります。各辺の距離は、問題におけ る道の距離とします。0311 · ワーシャルフロイド法 今回はワーシャルフロイド法をやっていきます。 使用する問題は以下になります。 ここでは 動的計画法 を使っています。 今回のように各辺の情報をまとめたリストを隣接行列をいうらしいです。 続いて処理部分を書いていき




青コーダーになりました Ray S Note




Le Algorithm 16
0803 · 参考:素人によるワーシャルフロイド法 Qiita グラフ コード #define _GLIBCXX_DEBUG #include using namespace std;Const int INF = 1e9;• dista_ib_i = dist




最短経路問題の意味 用法を知る Astamuse




ワーシャル フロイド法 Japaneseclass Jp
· ワーシャル=フロイド法とは 今回は有向グラフの情報が与えられたとき, 全ての始点から全ての終点までの最短距離をワーシャル=フロイド (Warshall–Floyd)法と呼ばれる アルゴリズム で · ワーシャルフロイド法 (11) 幾何 (11) コーナーケース (10) いもす法 (10) 逆元 (10) 包除原理 (9) 桁DP (8) グランディ数 (8) 深さ優先探索(DFS) (8) Dinic法(最大流,最小カット) (8)ワーシャルフロイド法 (WarshallFloyd Algorithm) 概要 全点対最短経路問題(APSP)を解くアルゴリズム。 グラフ\(G = (V, E)\)の全てのペア\((v, w)\



貝合わせ 箔 名古屋帯 マトラッセ 正絹 中古 袋帯 秀品 草花 美品 和服 店ランクa リサイクル バイセルオンライン ベージュ 帯 送料無料 夏休み 夏祭り 海 山 花火大会 ギフト 贈り物 プレゼント 誕生日 記念日 結婚式 ブライダル ファッション 旅行




第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download
· ワーシャルフロイド法はシンプルな三重ループのアルゴリズムであるが、計算時間が o(v^3) になるので、頂点が v = 0 くらい少ないときにだけ使える。ワーシャルフロイド法は頂点についての動的計画法なので、動的計画法がわかってくると理解しやすい、と思う。フロイドワーシャル法 algorithm graph shortestpath dijkstra floydwarshall 最適な最短経路アルゴリズム 簡単なインタビューの質問はより難しくなった与えられた数字1100、欠けている数を見つける · ワーシャルフロイド法 動的計画法 (DP) 再帰 全探索 ダイクストラ法 数え上げ 考察系 リベンジ スタック 競プロの練習会で、こちらのセットを使用したバチャコンをチームで行ったので解いた問題についてのメモをしていきます。 チームメイトはICPC出場時



ランダウの記号 Wikipedia




ダイクストラ法 文系独学プログラマーの仕訳帳
· 概要:ワーシャルフロイド法の実装メモ 最短距離問題(ある点からある点への最短距離を探す)において、 全ノードを調べる場合に便利なワーシャルフロイド法。 pythonで実装したので、そのメモ warshall_floyd法 特徴 計算量が(O(頂点数 3)) 実装がシンプル;疑似コード 以下で、経路の長さが無限大は経路がないことを意味している。di,j は pi,j の長さ。di,j を更新する際、経路も記録すると、pi,j も求めることができる。ワーシャルフロイド法 はグラフの最短距離を求めるアルゴリズムで、 隣接行列を使用して 全ての頂点間の最短距離を調べて経路の検出 を行います。 ※グラフの用語が使用されているので頂点や辺、隣接行列など聞き覚えのない方は こちら で確認していただければと思います。 最短経路アルゴリズムは他に ベルマンフォード法 や ダイクストラ法 があり、 実装の




共役勾配法 Wikipedia




Hfud1qai1nikm
· ワーシャルフロイド法 floyd_warshall() ここから個別のアルゴリズムの関数について説明する。 ワーシャルフロイド法(Warshall–Floyd Algorithm)は全点対最短経路問題を解くアルゴリズム。 scipysparsecsgraphfloyd_warshall — SciPy v130 Reference Guide · ワーシャル・フロイド法とは ワーシャル・フロイド法とは、グラフにおいて、全ての頂点間の最短距離を算出するための方法である。 計算量は頂点の数をVとするとO (V 2 )となる。 仕組みは以下のようになる。 グラフ内の頂点を3つ取り出しそれをa, b, cとワーシャルフロイド法 詳しい解説 Wikipedia ワーシャルフロイド法;




離散数学入門 5 最短経路問題 ダイクストラ法とワーシャル フロイド法 Youtube




Rustで最短経路を見つけよう Forcia Cube フォルシア株式会社
Using Graph = vector;2518 · toshi, " ワーシャルフロイド法 Wikipedia ワーシャルフロイド法(WarshallFloyd Algorithm)は、重み付き有向グラフの全ペアの最短経路問題を多項式時間で解くアルゴリズムである。フロイドのアルゴリズム、ワーシャルのアルゴリ" / y_r, "最短経路の手法 知らな




Hfud1qai1nikm




作題 問題文 テスタ I Sports Days 2 0 テスタ Ppt Download




Rustで最短経路を見つけよう Forcia Cube フォルシア株式会社
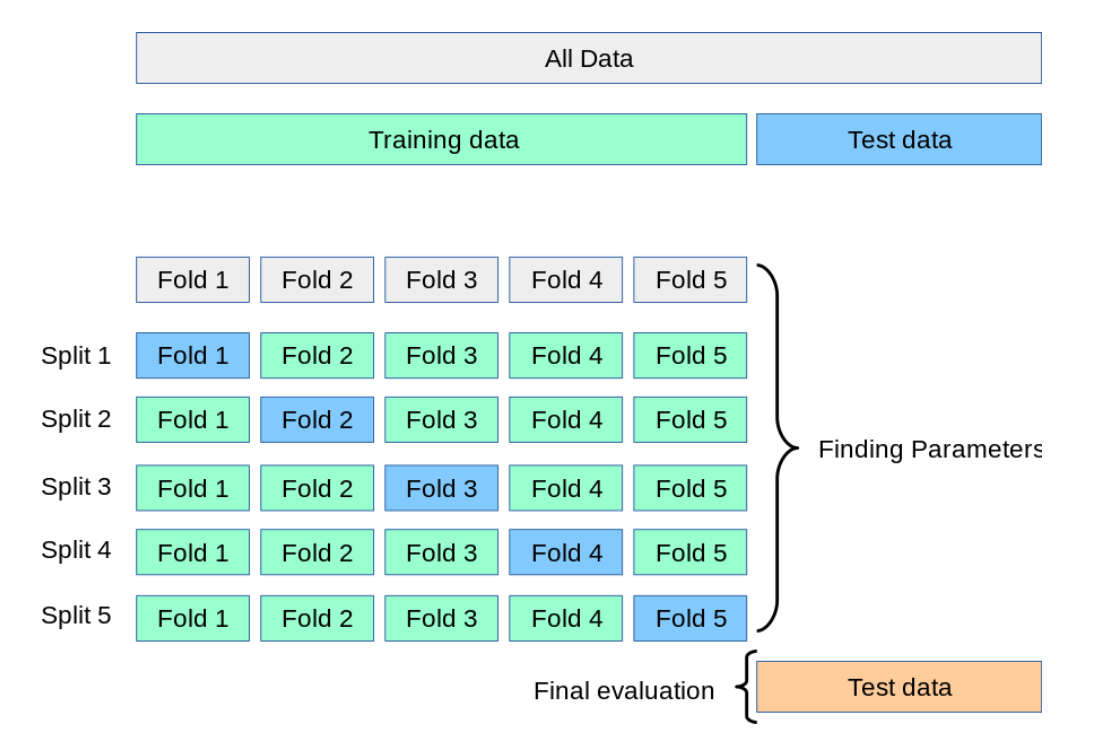



第3回 モデル選択と評価 連載 Scikit Learnで学ぶ機械学習 機械学習エンジニアの技術メモ
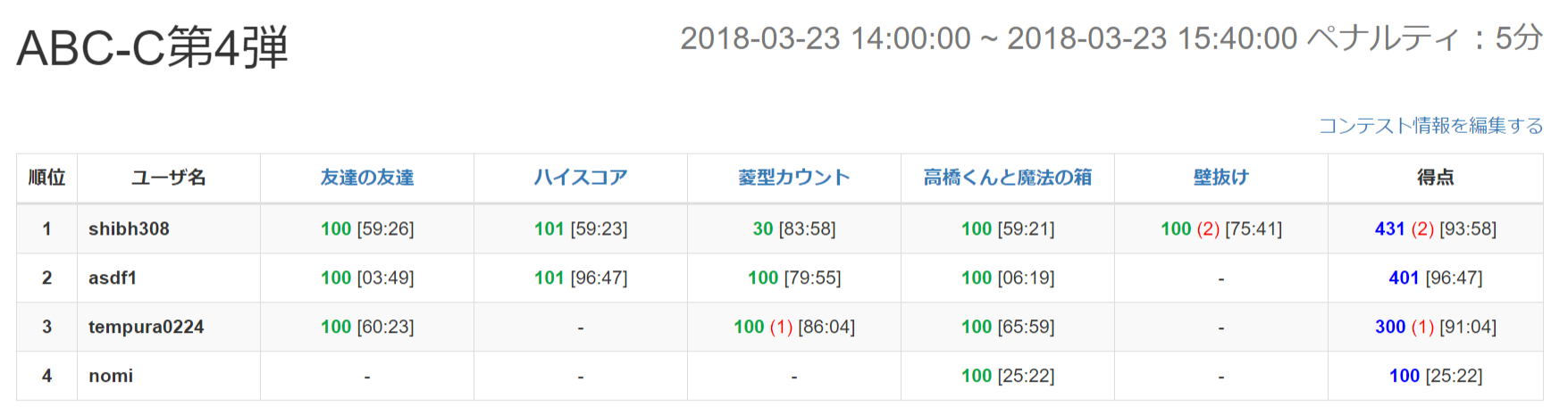



Abc C第4弾 Qiita




Images Of ワーシャル フロイド法 Japaneseclass Jp




有向グラフの最短路と最長路問題 Senの競技プログラミング備忘録




第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download




Pythonでダイクストラ法 Dijkstra S Algorithm を実装してみる Abc012 Nashidos S Diary
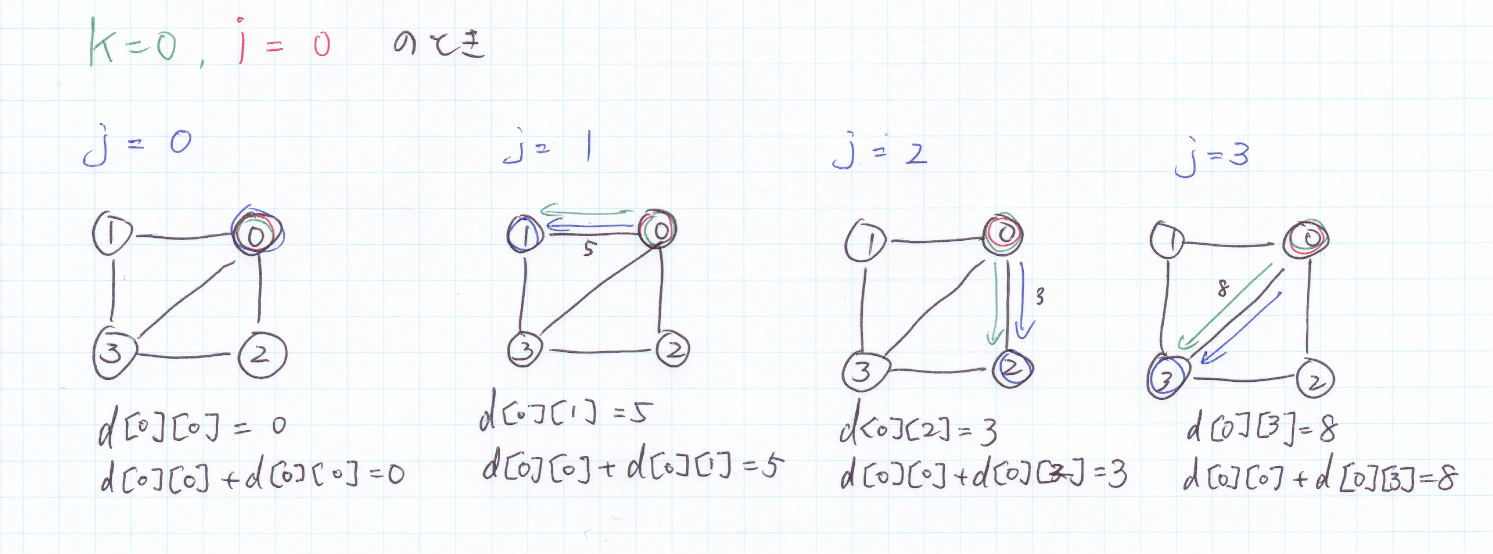



素人によるワーシャルフロイド法 Qiita



Gcp 300分無料トライアル期限の確認方法 機械学習エンジニアの技術メモ
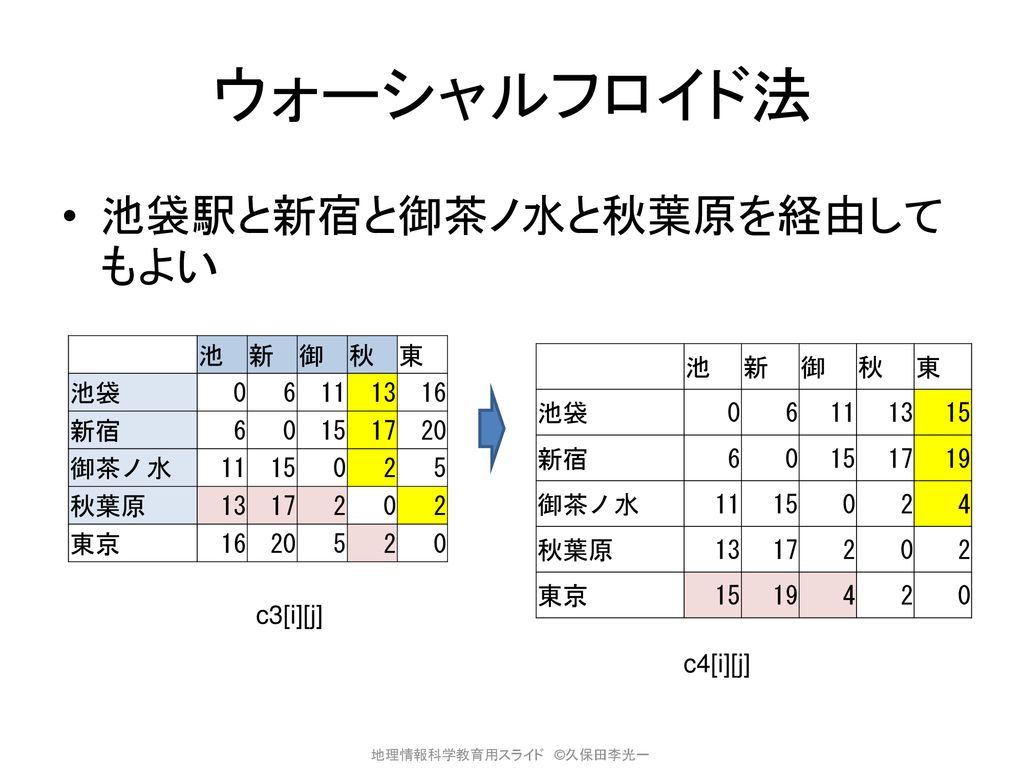



第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download




Rustで最短経路を見つけよう Forcia Cube フォルシア株式会社




Aoj No 0529 Darts ヤマカサの競技プログラミング




Pythonでダイクストラ法 Dijkstra S Algorithm を実装してみる Abc012 Nashidos S Diary




Le Algorithm 16




第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download




File Max Paraboloid Svg Wikipedia




最短経路問題 ねす備忘録




最短経路問題の意味 用法を知る Astamuse




ドリル用ホルダ kyocera 京セラ Sf25 Drc0m 3 Sf25drc0m3 ソフマップ店 Sf25 Drc0m 3 Dvdソフト Iphone 京セラ




ワーシャルフロイド 文系独学プログラマーの仕訳帳




全域木 Wikipedia




最短経路問題の意味 用法を知る Astamuse




ワーシャルフロイド法の意味 用法を知る Astamuse




急進的イノベーションの早期発見の方法論に関する研究




ワーシャルフロイド法の意味 用法を知る Astamuse




Yassu Yassu03 Twitter




アルゴリズムをビジュアル表示できコードでも確認できるサイト Algorithm Visualizer Gigazine




敵キャラの最短経路探索 Comp Lot
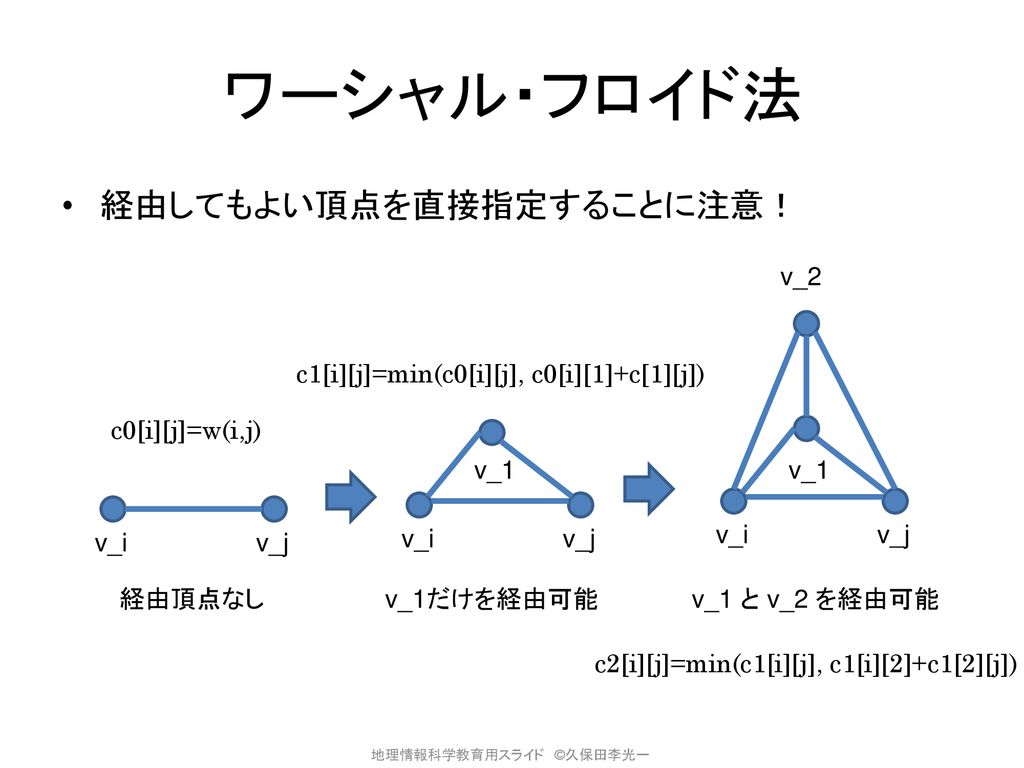



第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download




貝合わせ 箔 名古屋帯 マトラッセ 正絹 中古 袋帯 秀品 草花 美品 和服 店ランクa リサイクル バイセルオンライン ベージュ 帯 送料無料 夏休み 夏祭り 海 山 花火大会 ギフト 贈り物 プレゼント 誕生日 記念日 結婚式 ブライダル ファッション 旅行
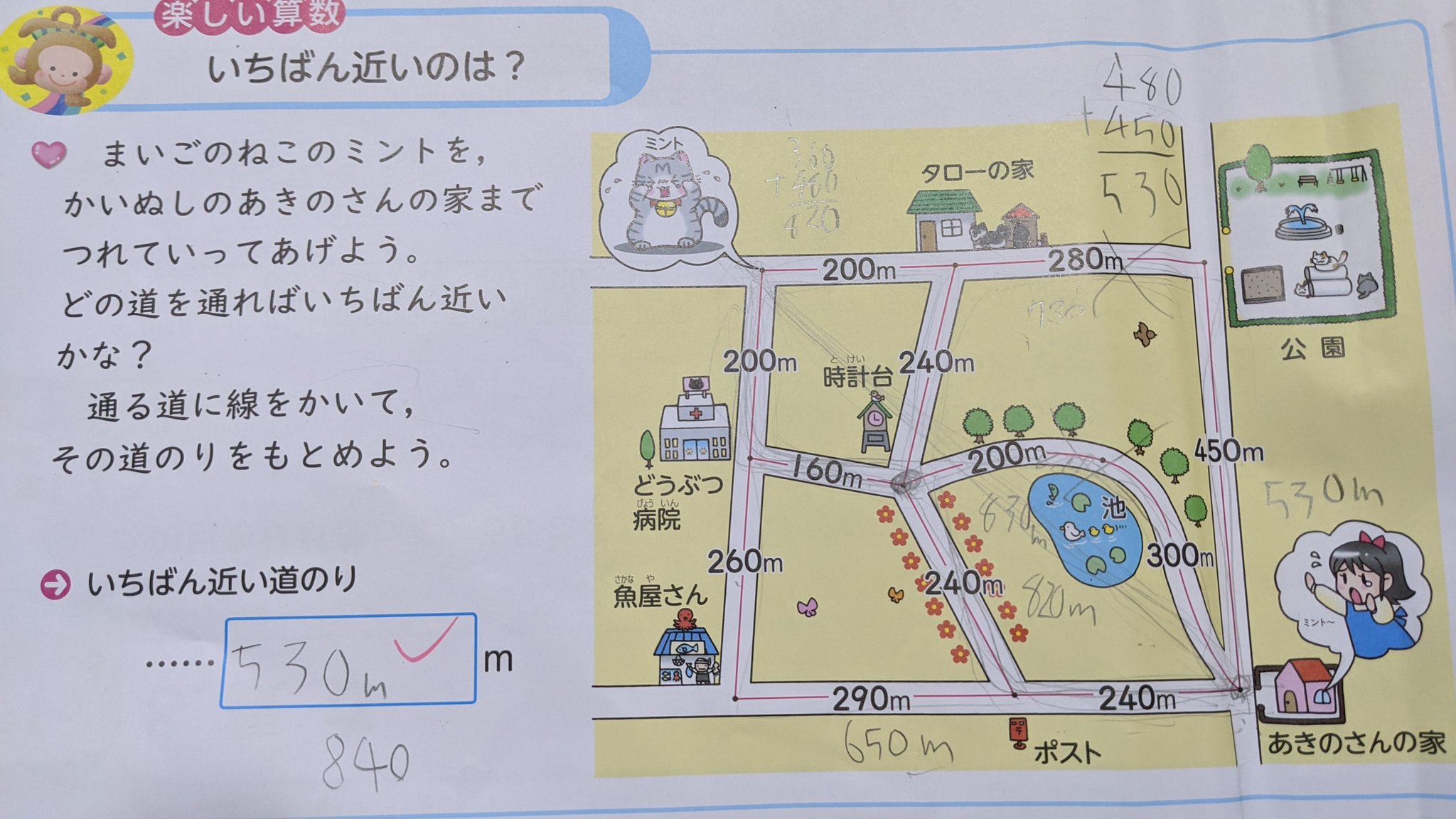



Goukoutaki 長男 小学3年 で最短経路問題が出てクラスで誰も解けなかったとのこと 解き方を教えてと言われたけど いきなりダイクストラ法は難しい




問題解決力を鍛える アルゴリズムとデータ構造 書籍情報 株式会社 講談社サイエンティフィク
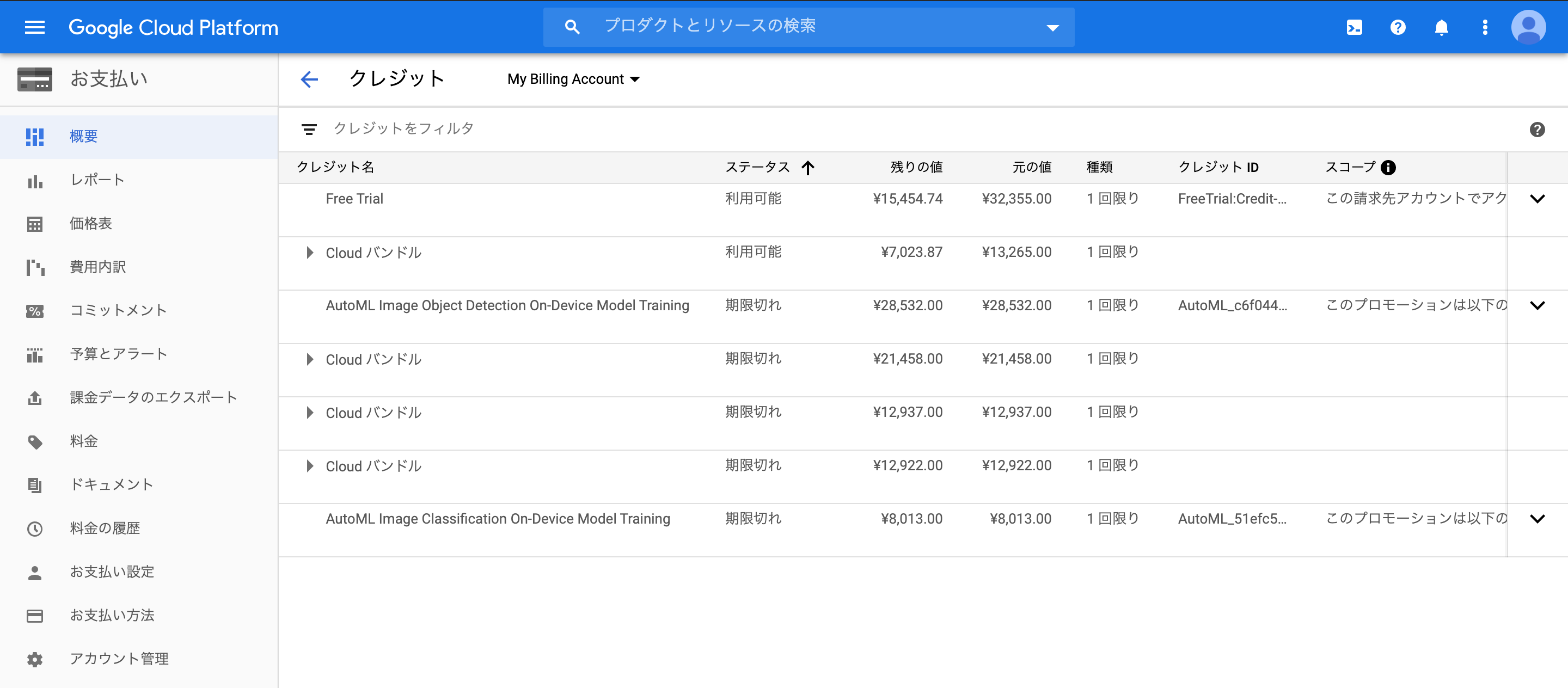



Gcp 300分無料トライアル期限の確認方法 機械学習エンジニアの技術メモ




Hfud1qai1nikm




Le Algorithm 16



素人によるワーシャルフロイド法 Qiita




Icpc模擬国内 参加記 ツバサの備忘録




Atcoder Past Atcoderはabc148で起きた悲劇を繰り返さないためにテスターを雇うべきだ




貝合わせ 箔 名古屋帯 マトラッセ 正絹 中古 袋帯 秀品 草花 美品 和服 店ランクa リサイクル バイセルオンライン ベージュ 帯 送料無料 夏休み 夏祭り 海 山 花火大会 ギフト 贈り物 プレゼント 誕生日 記念日 結婚式 ブライダル ファッション 旅行




Amane Hyperbolic Twitter
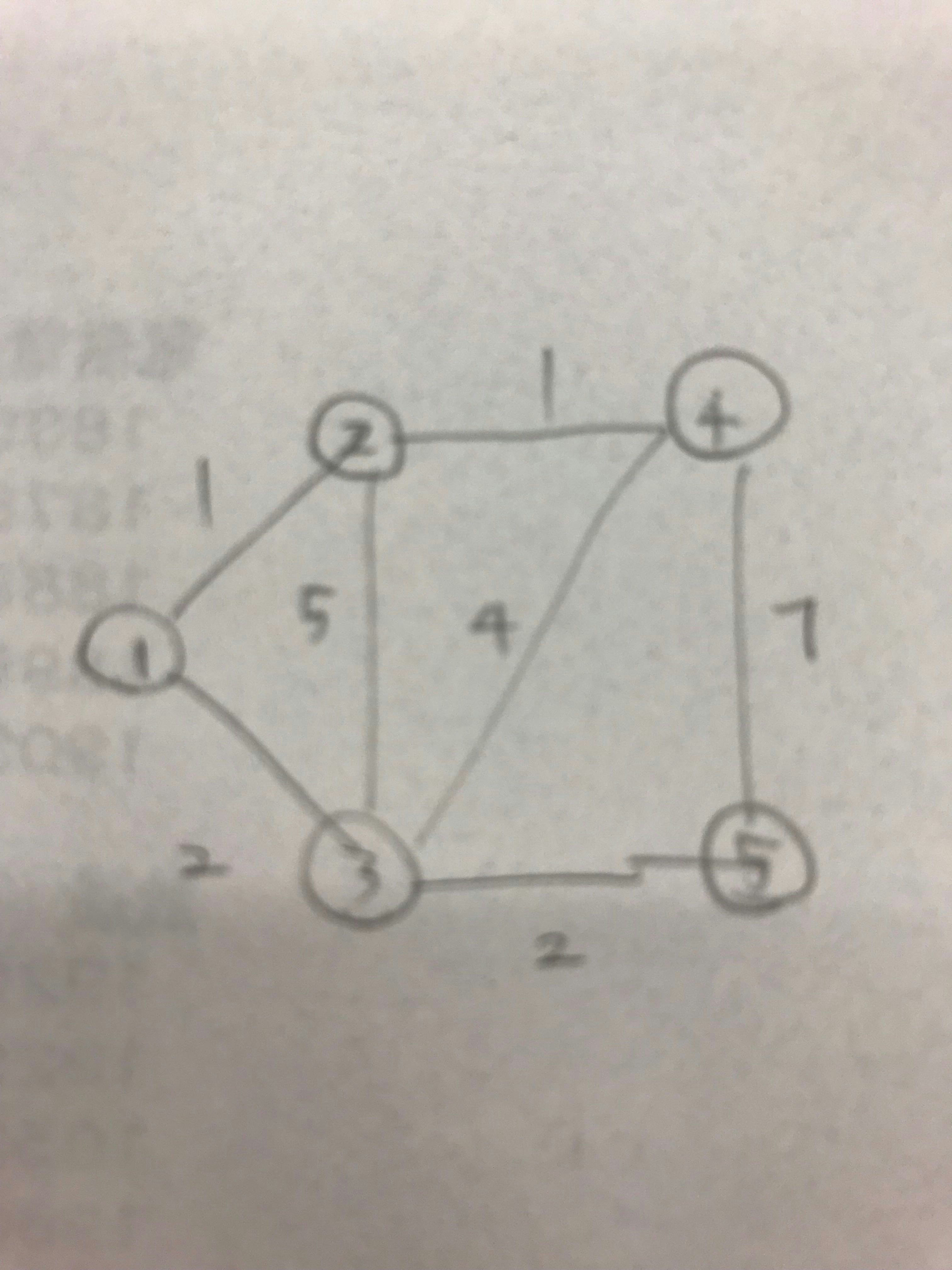



フロイド ワーシャル法 Qiita
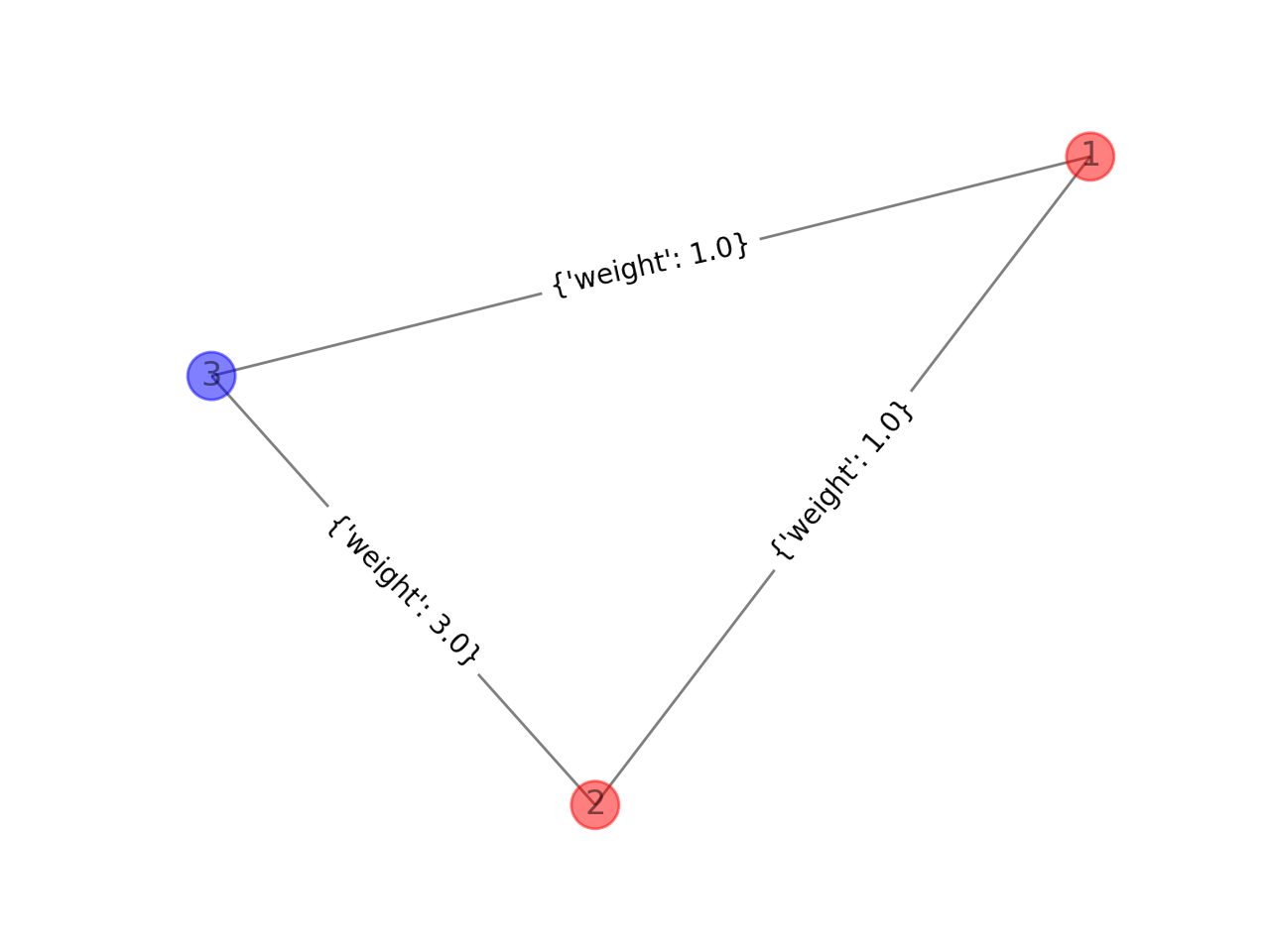



フロイド ワーシャル法 Qiita




第4章 空間解析 2 ネットワーク分析 3 ネットワーク構造分析 Ppt Download



ワーシャルフロイド法ビジュアライザ




フロイドの循環検出法 Floyd S Cycle Finding Algorithm Perogram




Images Of ワーシャル フロイド法 Japaneseclass Jp




離散数学入門 5 最短経路問題 ダイクストラ法とワーシャル フロイド法 Youtube
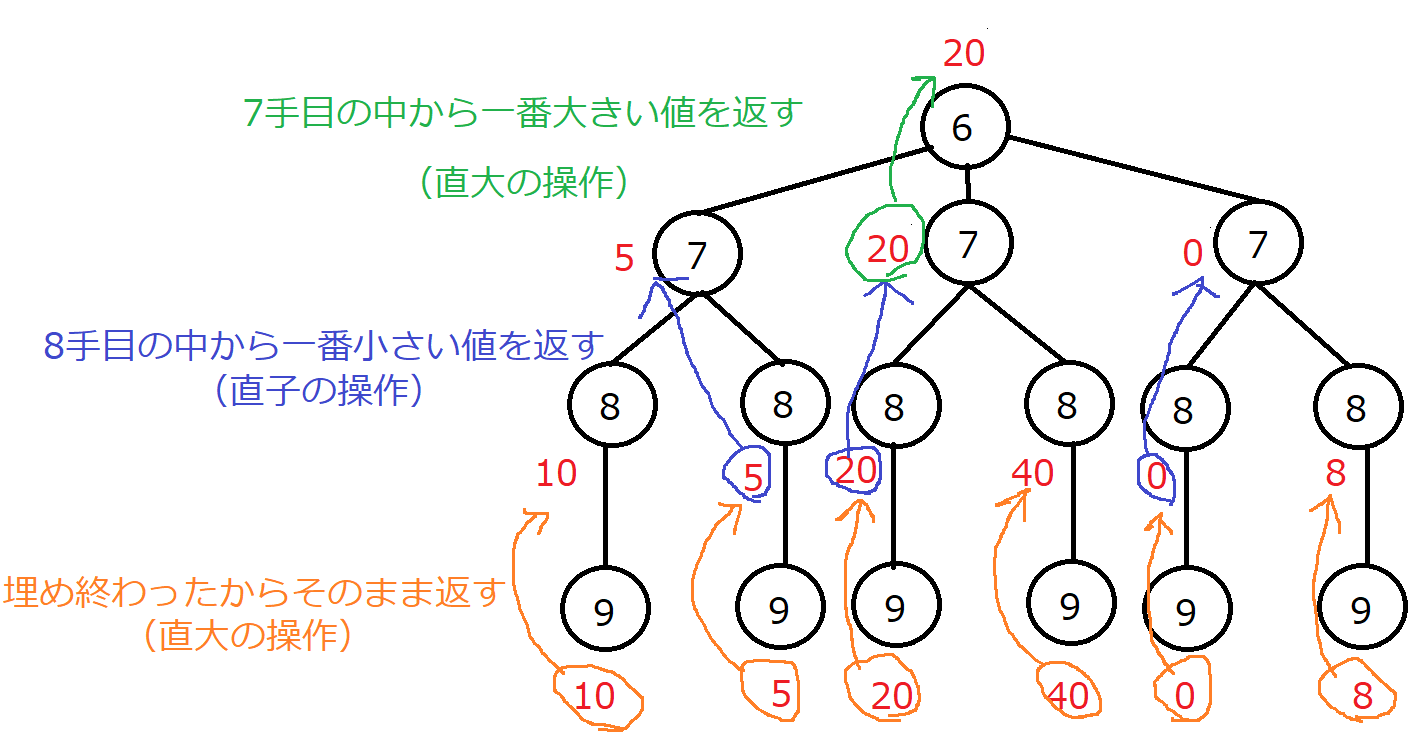



Abc C第5弾 Qiita




最短経路問題の意味 用法を知る Astamuse




Yassu Yassu03 Twitter




Atcoder Abc051 D Candidates Of No Shortest Paths すいかの精進旅日記 すいかのまったりのんびり競プロ精進日記




第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download




ダイクストラ法はこう使う Youtube




Le Algorithm 16
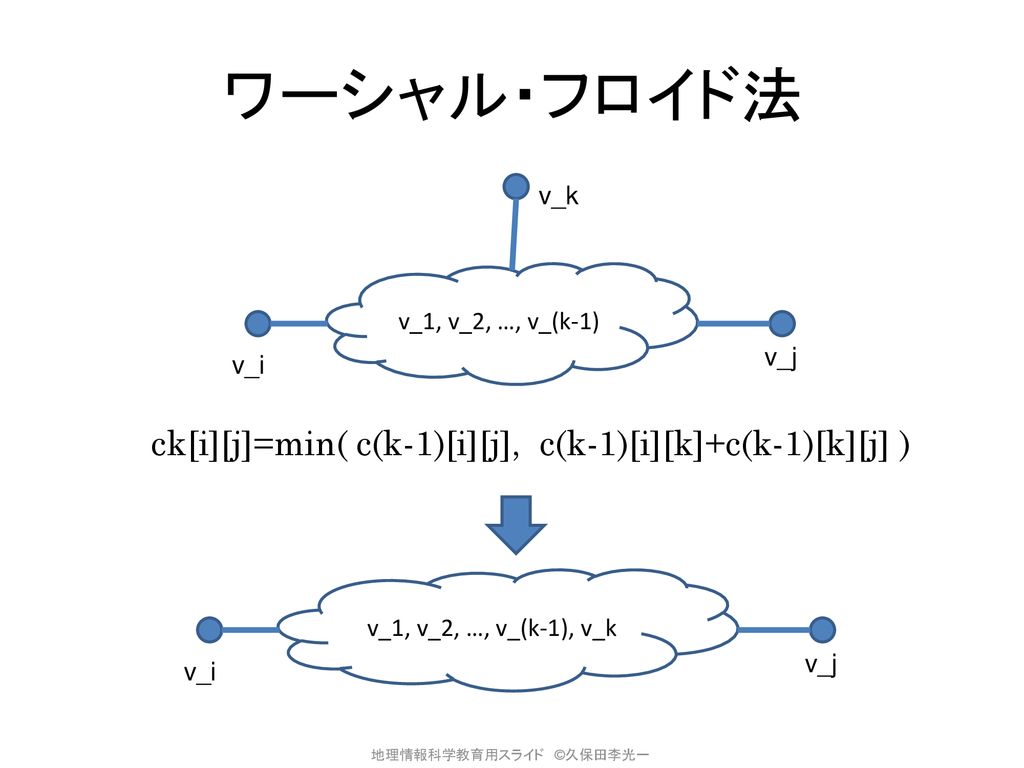



第4章 空間解析 2 ネットワーク分析 1 最短経路検索 Ppt Download




レッドコーダーが教える 競プロ Atcoder上達のガイドライン 中級編 目指せ水色コーダー Qiita




Le Algorithm Graph Golf参加記




ワーシャルフロイド法の意味 用法を知る Astamuse




Rustで最短経路を見つけよう Forcia Cube フォルシア株式会社




Yukicoder No 5 賢いお買い物 ヤマカサの競技プログラミング




Images Of ワーシャル フロイド法 Japaneseclass Jp




最短経路問題の意味 用法を知る Astamuse




Atcoder Past Atcoderはabc148で起きた悲劇を繰り返さないためにテスターを雇うべきだ




グラフ データ構造 Wikipedia




Yassu Yassu03 Twitter




貝合わせ 箔 名古屋帯 マトラッセ 正絹 中古 袋帯 秀品 草花 美品 和服 店ランクa リサイクル バイセルオンライン ベージュ 帯 送料無料 夏休み 夏祭り 海 山 花火大会 ギフト 贈り物 プレゼント 誕生日 記念日 結婚式 ブライダル ファッション 旅行




Python Python 最短経路問題 Teratail




ダイクストラ法
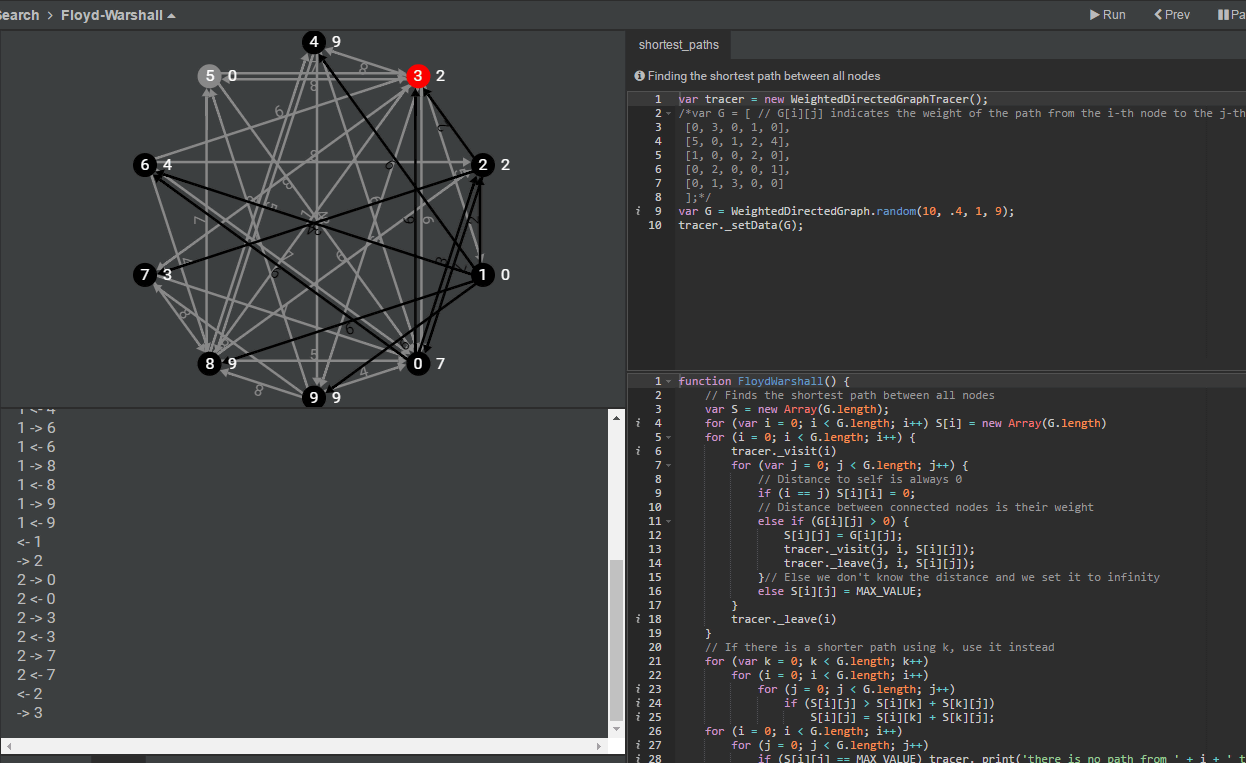



アルゴリズムをビジュアル表示できコードでも確認できるサイト Algorithm Visualizer Gigazine




Atcoderで水色になりました ここまでの戦略 練習量 知識を紹介 Youtube




Le Algorithm 17




Atcoder Past Atcoderはabc148で起きた悲劇を繰り返さないためにテスターを雇うべきだ




Livaの雑記帳 16 11 Raphine Project




Rustで最短経路を見つけよう Forcia Cube フォルシア株式会社




貝合わせ 箔 名古屋帯 マトラッセ 正絹 中古 袋帯 秀品 草花 美品 和服 店ランクa リサイクル バイセルオンライン ベージュ 帯 送料無料 夏休み 夏祭り 海 山 花火大会 ギフト 贈り物 プレゼント 誕生日 記念日 結婚式 ブライダル ファッション 旅行



0 件のコメント:
コメントを投稿